Wishful Coding

The other day I was helping my brother with the second version of his performance installation DEMARRAGE, which involves serving a web page from an ESP32 that displays the energy produced by two dynamo bikes.

For this page we wanted a simple gauge, so I figured a solution would be an internet search away. But all the examples I found seemed really complicated, with verbose markup, opaque CSS, and sometimes an entire JS library. So I decidede to make my own.

My goals were

• Very minimal HTML without any extra dummy elements.
• CSS that is easy to understand and modify.
• Easy to update the value from JS.
• A gauge of 270° rather than a semi-circle.
• (browser compat was not a goal)

The HTML is as simple as it gets, just a div with custom properties and the textual value.

<div class="gauge" style="--value:0.3; font-size:2rem;">30%</div>

Conceptually, the CSS isn’t very complicated either.

• set the size of the gauge div
• set a border-radius to make a circle
• draw a conic-gradiant to make a pie-chart
• draw a radial-gradient to cut out the center
• center the text with text-align and line-height

The code CSS makes use of calc and var, primarily to adjust the conic-gradient angle based on a custom property, but also to parameterize the dimensions of the gauge. This means you can override --size and friends to style the gauge without changing hardcoded values.

.gauge {
  --size: 200px;
  --cutout: 50%;
  --color: red;
  --background: white;
  width:var(--size);
  height:var(--size);
  border-radius:calc(var(--size) / 2);
  background:
    radial-gradient(
        var(--background) 0 var(--cutout),
        transparent var(--cutout) 100%),
    conic-gradient(from -135deg, 
        var(--color) calc(270deg*var(--value)),
        grey calc(270deg*var(--value)) 270deg, 
        transparent 270deg);
  text-align: center;
  line-height: var(--size);
}

The JavaScript for changing the gauge value is pretty simple too, given some gauge DOM element el you can change the gauge value and text content by simply doing

el.style.setProperty("--value", 0.8)
el.innerHTML = "80%"

Below is a codepen to play with the code. I hope it’s useful to someone.

See the Pen Pure CSS gauge by Pepijn de Vos (@pepijndevos) on CodePen.

After a bit of chatting on the Recurse Center Zulip, I came up with the following alternative gradients that provide a 3D effect or that goes from red to orange to green. The 3D one works by adding a transparent black gradient to the radial part. The colourful one works by making a fixed backdrop and a transparent-grey gradient on top that reveals the underlying one.

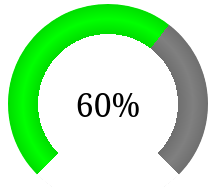
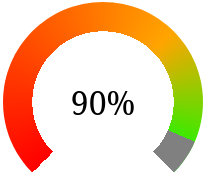
  background:
    conic-gradient(from -135deg,
      transparent 270deg,
      white 270deg),
    radial-gradient(
      var(--background) 0 var(--cutout),
      #0002 calc(var(--cutout)),
      #0000 calc(var(--cutout) + 15px),
      #0002 calc(var(--cutout) + 30px),
      #0000 calc(var(--cutout) + 30px) 100%),
    conic-gradient(from -135deg,
      var(--color) calc(270deg*var(--value)),
      grey calc(270deg*var(--value)) 270deg,
      transparent 270deg);

  background:
    radial-gradient(
      var(--background) 0 var(--cutout),
      transparent var(--cutout) 100%),
    conic-gradient(from -135deg,
      transparent calc(270deg*var(--value)),
      grey calc(270deg*var(--value)) 270deg,
      transparent 270deg),
    conic-gradient(from -135deg,
      red 0,
      orange 135deg,
      lime 270deg,
      transparent 270deg);

I came across a random tweet, found a Wikipedia page and bumped into some smart people and long story short, apparently compression is equivalent to general intelligence.

So, how do you build ChatGPT with data compression? What if you compress a large corpus of text to build up the encoding table, then you compress your prompt and append some random data and decompress the random data, and hope it decompresses to something sensible.

It feels vaguely similar to diffusion, but what do I know. Look, this is just a dumb idea, let’s just see what happens ok? Well, here is my progress so far. It’s kind of whack but it’s hilarious to me that it produces something resembling words.

import nltk
import lzma
import random

my_filters = [
    {"id": lzma.FILTER_LZMA2, "preset": 9 | lzma.PRESET_EXTREME},
]
lzc = lzma.LZMACompressor(lzma.FORMAT_RAW, filters=my_filters)

corp = nltk.corpus.reuters.raw().encode()
out1 = lzc.compress(corp)

corp = ' '.join(nltk.corpus.brown.words()).encode()
out2 = lzc.compress(corp)

corp = nltk.corpus.gutenberg.raw().encode()
out3 = lzc.compress(corp)

out_end = lzc.flush()

lzd = lzma.LZMADecompressor(lzma.FORMAT_RAW, filters=my_filters)

lzd.decompress(out1)
lzd.decompress(out2)
lzd.decompress(out3)
# mess around to avoid LZMAError: Corrupt input data
lzd.decompress(out_end[:-344])
# insert prompt????
print(lzd.decompress(random.randbytes(50)).decode(errors="ignore"))

Here are a few runs. Note how the start is always , and tri, usually completing it into some word. Are we doing some primitive accidental “prompting” or just flushing the buffer? Either way, not bad for mere seconds of “training”!

$ python train.py 
, and triof billioerse,
But
ht and see th,
Thy smile, in to be happy,
Wmson,
Over tout as aThy smile;t as aThyrged in
 
ent, foldehe snoion since how long,
my roomr? Is ic books 

$ python train.py 
, and triompact, sca,
Take deepcky fouy vitaliz  bodiehow there i,
Nor drummiwisibly wile of the-ations, dutway?
Yet ld woman'okesmanall whoy slow bekesmanalle me 

$ python train.py 
, and tri billions of the boftier, faie no acqutory's dazzd haOr that thpages:
(Sometimeseathe ihern, Sounte, fld Turkey n one,
Worlseathe Border Minstrelsy,ine, New-Ene Queen.

'Thelicate l

$ python train.py 
, and tri, sleepinlke babes  bent,
Abird;
Forhis fair n!
By thea mystic strangehe gifts ofhe body aering
 t: I haue a lugs whipageantuperb-fnz

$ python train.py 
, and triions of b--n the gra, with
e open the countless buAnd bid theng;
Billi  toward you.i ally undya Songs

To f Death, istas of was mar to be UY 9,30

In this digital age so much of our information is only on the internet, and it’s hard to predict how much of it would survive another Carrington event. So what if we engrave all of the information on the internet in stone? We have clay tablets dating back thousands of years, so if we want to preserve our knowledge for the millenia to come, it’s a time-proven method.

That’s it. That’s the plan. “set in stone” Wikipedia, literally. I know it sounds crazy and I don’t have any illusions about completing the project, but it seems a fun mix of art project and potentially my biggest contribution to the persistence of human kind haha

But how do I go about doing this? I want to automate it as much as possible, but it also has to be super durable and some amount of authentic. Like, if you’re going for pure efficiency and inforation density you’d maybe engrave binary into acrylic, but what’s the fun in that. There are so many remaining options from laser engraving slate to CNC routing clay tablets. Let’s just research and try some?

CNC engraving clay tablets

I started watching a bunch of youtube videos about low fire backyard pottery, where people make pottery on their own improvised coal furnaces and such. Some things I learned:

• get clay and mix in sand to make it less prone to exploding
• dry really really really well
• stick it in a bunch of coal and hope for the best

So I started making my clay tablet by mixing sand into the clay and adding water. Then I used (wet) planks to make the tablet as flat as possible.

Then I copied a wikipedia page into a text file and used hf2gcode to make gcode:

text=$(python - $1 <<END
import unidecode, sys
with open(sys.argv[1]) as f:
    print(unidecode.unidecode(f.read()))
END
)
echo "$text" | fold -w 20 | ./src/hf2gcode -s 0.3 -n 12

After letting the clay dry and with my gcode in hand I went to Tkkrlab to try to CNC it. I used bCNC for this. The first try chipped off some bits, so I sprayed some water to make it more soft. But the text was way too small, so I redid the gcode with a bigger font and only the first paragraph of the wikipedia page.

With a bigger font size and regular water spraying I was making good progress, untill the bit started cutting deeper and deeper. Despite my best efforts the tablet wasn’t flat enough, so I had to stop, readjust the CNC, and do some hacky maneuvers to start the job from that point. Success?! Some parts were barely touching, but it’s something!

So I went back home and put it in the oven to dry further. First at below 100, then at 150, and then cranking it all the way up. I guess I was too impatient because it exploded.

Lessons learned

• I need to be way more patient with drying (and possibly avoid making bubbles?)
• It needs to be way flatter (or I need to measure and compensate)
• It looks amazing
• Information density is super low

So I’m a bit torn, the first two items are probably solvable, and I really love how it looks, but at this font size it can barely fit a paragraph. With a beter process I can maybe reduce it a little bit, in particular the line height is quite excessive, but it’s just not going to fit an entire wikipedia page.

Do I continue pushing this, or do I try something else? I think I might try what laser engraving slate looks like once the laser cutter at Tkkrlab is back in operation.