Problem
In a hall, two rows of 5 10W 12V lamps are connected in parallel over a distance of 10m, powered by two different 12V power supplies. The setup is like below.
The one is a big good old transformer that outputs 12VAC at 50Hz. The other is a switching mode power supply with a switching frequency of 100KHz.
The string of lamps powered by the transformer have an equal brightness, while the string powered by the switching mode power supply diminishes, with the 5th lamp only glowing dimly.
What is going on here? Answers below, but think about it for a minute.
Investigation
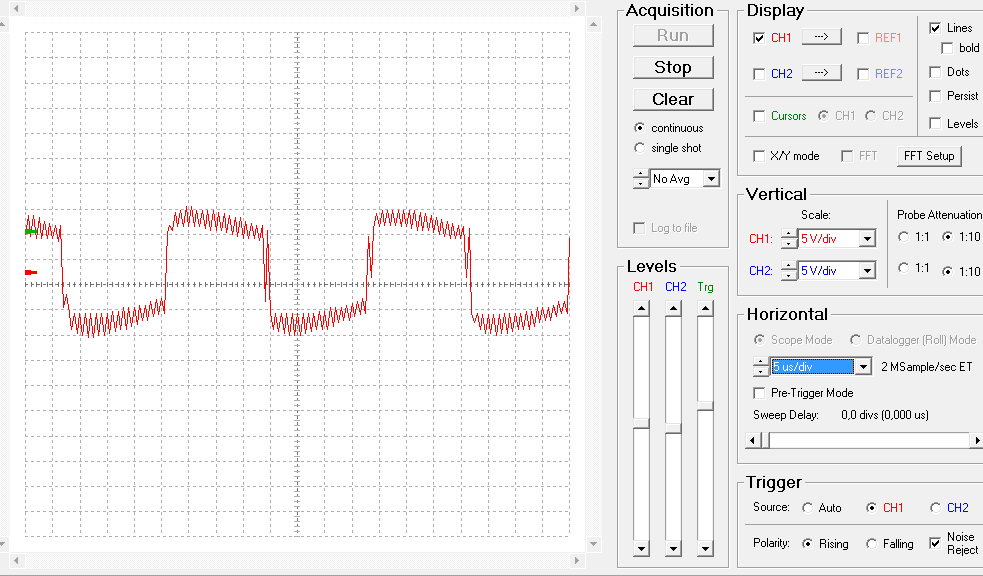
The first thing I did when I saw these lamps is connect an oscilloscope to the output of the supplies.
The transformer outputs a 50HZ 12VAC sine wave as expected. The other supply appears to be a switching supply. It outputs a 100KHz square wave with some high-frequency ringing. If you zoom out, it has a 50Hz envelope.
Solution
Since the only difference between the two setups is the frequency, the resistance of the wires is apparently negligible and the only thing that could have influence is the inductance of the wire.
Using an online calculator, I found that the inductance of 4m (10m back and forth divided by 5) copper wire is 3μH, and the resistance of the lamps follows from their rated voltage and wattage.
\[\begin{aligned} W&=VI=\frac{V^2}{R}\\ R&=\frac{V^2}{W}=14.4\Omega \end{aligned}\]So a more accurate representation of the situation is below.
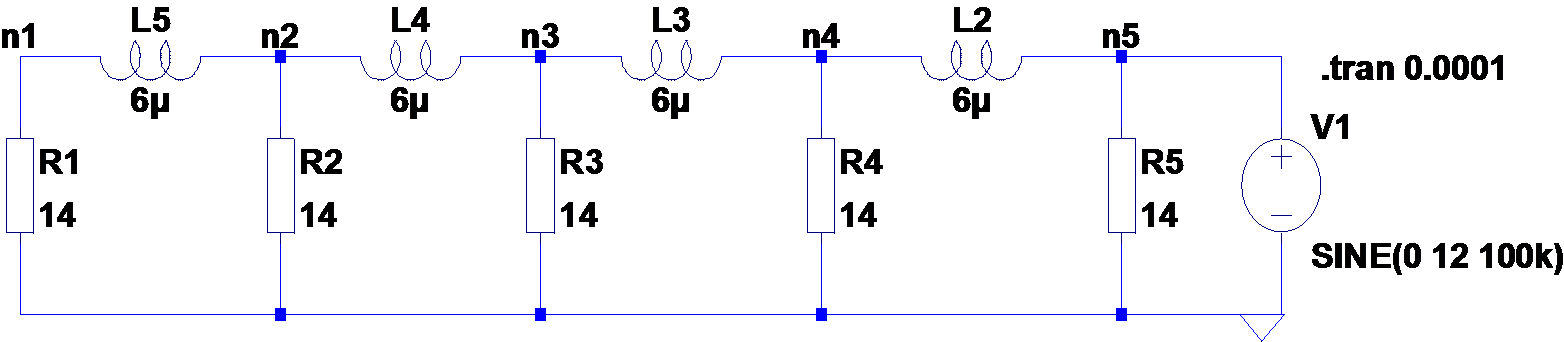
From this the AC voltage for any of the lamps can be calculated. For a single lamp at the end of a 10m wire, it would mean
\[\begin{aligned} V_{n1}(j\omega)&=\frac{V_{in}R_1}{j\omega L_5+R_1}\\ V_{n1}(j\cdot 2\pi 100000)&=\frac{12\cdot 14}{j\cdot 628318 \cdot 30\cdot 10^{-6}+14}\\ V_{n1}(j\cdot 628318)&=\frac{168}{j\cdot 18+14}\\ \left|V_{n1}(j\cdot 628318)\right|&=\frac{168}{\sqrt{18^2+14^2}}=7V\\ \end{aligned}\]For all 5 lamps it gets a bit hairy.
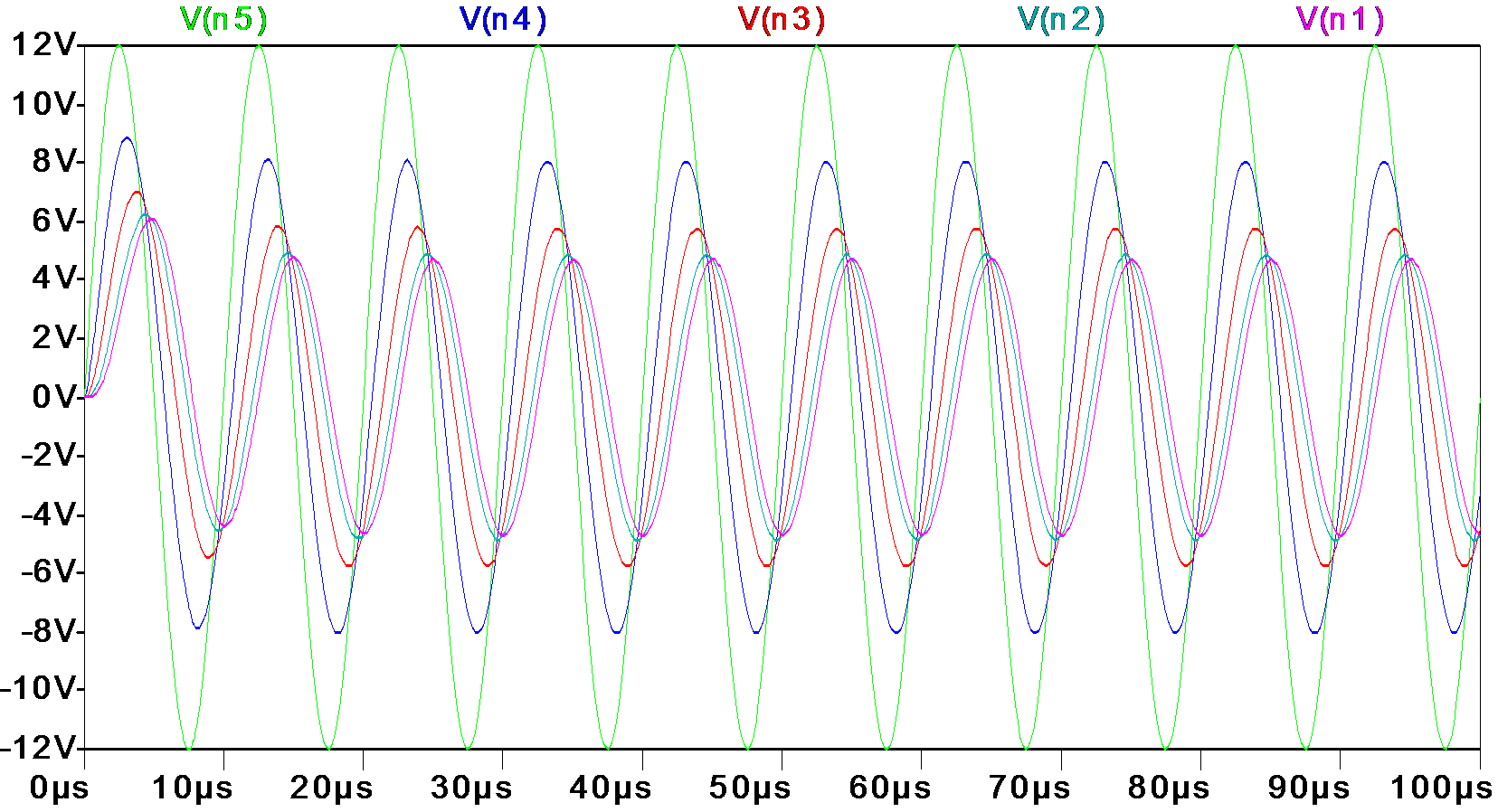
\[\begin{aligned} V_{n1}(j\omega)&=V_{n2}(j\omega)\frac{R_1}{j\omega L_5+R_1}\\ V_{n2}(j\omega)&=V_{n3}(j\omega)\frac{R_2//(R_1+j\omega L_5)}{R_2//(R_1+j\omega L_5)+j\omega L_4}\\ V_{n3}(j\omega)&=V_{n4}\frac{\ldots}{\ldots+j\omega L_3}\\ V_{n4}(j\omega)&=V_{n5}\frac{\ldots}{\ldots+j\omega L_2}\\ V_{n5}(j\omega)&=12V \end{aligned}\]But simulation gives the following result, only 4V on the lamp at the end.