Wishful Coding

You know these helium balloons? They float because helium is lighter, less dense then air. You know what is even lighter than air? No air at all!

I came across the idea on this website, where he notes

I haven’t done any math, but I assume this isn’t feasible at the present time.

I have done some math, or rather, asked Wolfram Alpha.

So, first of all, how heavy is a cubic meter of air anyaway?

Ok, so our balloon can weigh just over a kilo and still float. But what is the surface area of a balloon of that size?

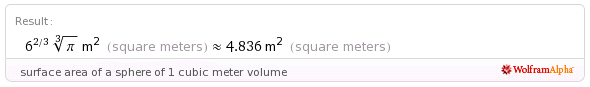
Almost five square meter. So with one kilo of matter, we need to make a balloon of nearly 5 square meter surface area.

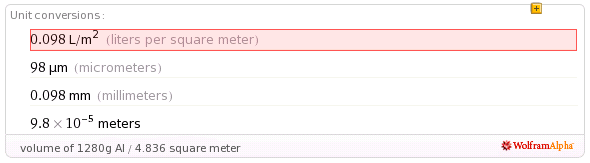
Aww, not looking good. If we use aluminum¹, we can make a shell of a tenth of a millimeter thick. This shell will have to resist 1 bar, which equals 10 newton per square centimeter.

I just picked this up from Wikipedia, but presumably this means the stress on the shell will be 3162 newton per square millimeter.

Now, remember that this is a vacuum, so while a pressurized balloon retains it shape because of the pressure, the biggest problem with our vacuum balloon is the buckling force.

The smallest dent, a gust of wind, or even gravity itself, will cause the balloon to implode. I asked my dad², and he asked his engineer, how to calculate this force. Third order magic.