My dad likes to argue with flat earthers on Facebook, so I decided to steel man a consistent flat earth theory. The premise is simple: you just take a 3D azimuthal equidistant projection of the spherical world and rewrite physics in the new coordinate system. This is what it looks like:
This is very similar to a geocentric model of the universe, it’s not fundamentally wrong to choose earth as your reference frame, just very inconvenient for describing orbits around the sun. In the same way it’s not fundamentally wrong to assume the earth is flat, but it warps the rest of the universe in strange ways.
For example, here is a round earth. We observe ships disappearing over the horizon, and we observe day and night.

Most flat earth models don’t tend to have satisfactory explanations for sunset, things disappearing behind the horizon, and eclipses. The solution is simple: light curves away from the earth. At some point sunlight curves back into space.
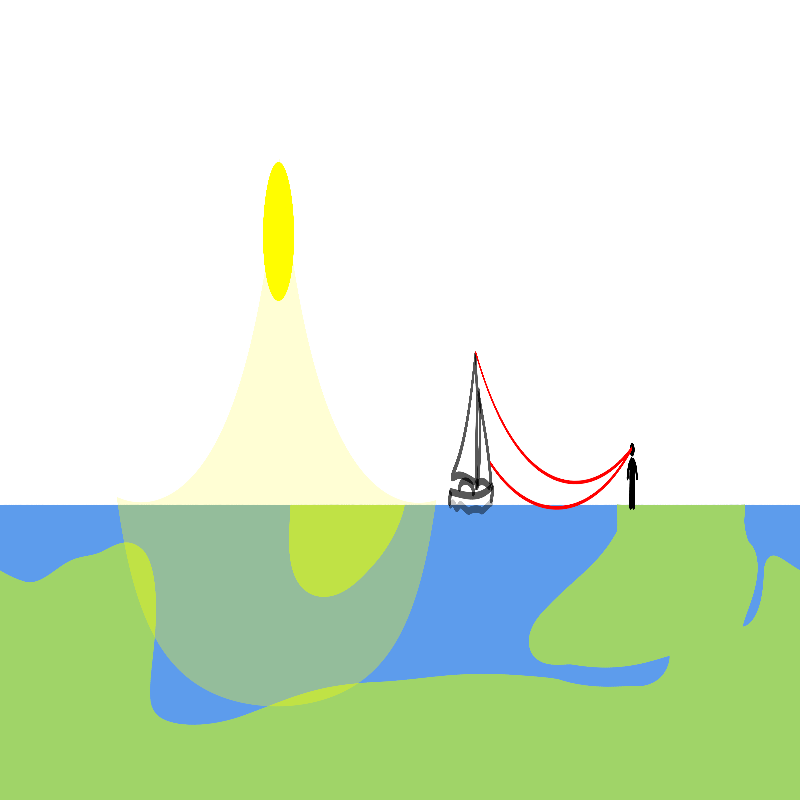
In this model the sun is still further away than the moon, so a solar eclipse is simply the moon moving in front of the sun as usual. In a lunar eclipse, the light of the sun has to bend so deep that it would touch the earth before it could bend back up to the moon.
A lovely result from this flat earth model is that it clearly answers the questions what is below the earth: the singularity. Even better is that the density of the earth goes down the closer you get to the singularity, meaning the earth is in a sense hollow. Finally a grand unifying theory of hollow earth and flat earth models!
The downside of this model that physics isn’t independent of location and direction. For example the atmosphere is denser in the middle of the disk. A simple equation like \(F=ma\) becomes hellishly complicated if you want it to work everywhere. There is also a magic Pacman teleportation point on the south pole.
This model is internally consistent and impossible to falsify since it is simply a coordinate transform of conventional physics. You can’t make any observations that would disagree with the model and agree with a spherical model since they are the same universe. It is not possible to measure which way of looking at things is “real” because all your observations and tools are curved in the same way. Therefore, you could interpret the earth to be flat.
With the combined skills in Blender and mathematics of me and my brother, we managed to implement the flat earth coordinate transformation in Blender geometry nodes so that you can make a 3D model and see what it looks like on a flat earth.
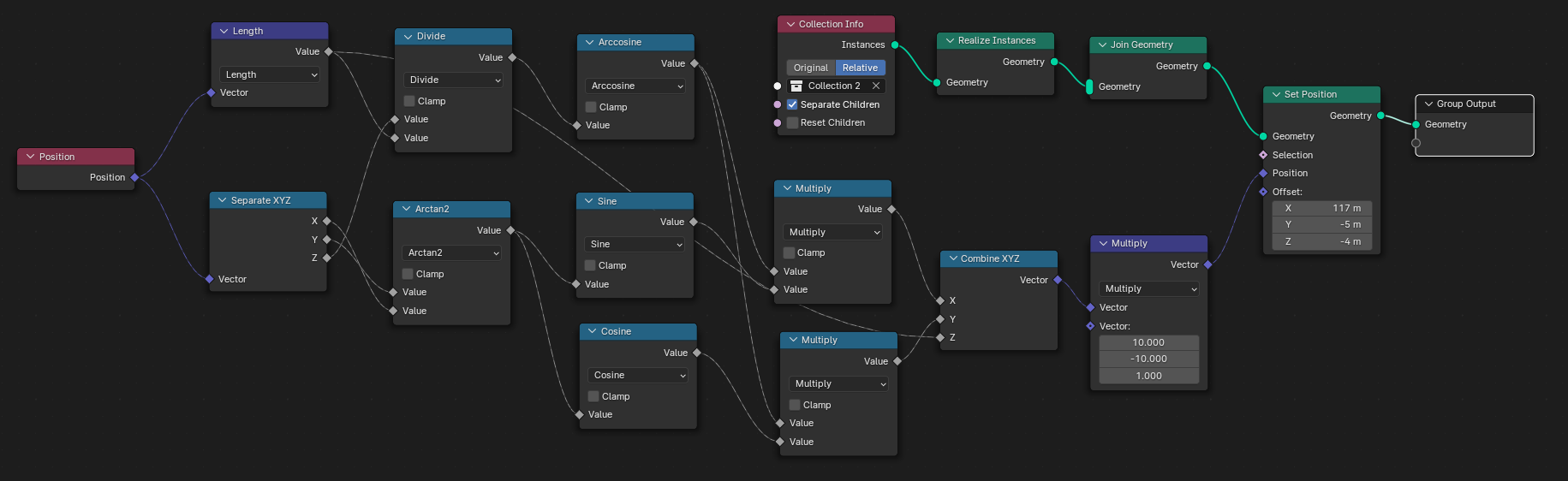
We struggled to get lighting to work since Blender would render linear light after the transform, so instead we drew physical light cones with luminescent hemispheres that pass through the transform correctly. Unfortunately this means we can’t render eclipses, but the upside is you can really see the wild curves light makes on a flat earth.
We’ve theorized that it might be possible to bake lighting into the texture as is commonly done for video games, but it’s nice weather outside so we pressed render and left eclipses as an exercise to the reader.
